I - Notions de base (cliquer
pour télécharger le document PDF correspondant au
chapitre : 85 Ko)
- Traitement d'images (I)
- Traitement d'images (II)
- Quattre démarches en traitement d'image
- Définition de la Morphologie Mathématique
- Structures de base
- Concepts premiers
- Exemples de treillis
- Treillis de fonctions
- Treillis de partitions
- Atomes, co-premiers et complements
- Sup-générateurs, distributivité
- Caractérisation des treilles P(E)
- Notion de dualité
- Autodualité
- Comparaison entre entrée et sortie
- Treillis d'opérateurs
- Notion de résidu en morphologie
- Classification des residus
- Transformations morphologiques et homothéties
- Mesures et courbes
|
II - Dilatation, Erosion
(cliquer pour télécharger le document PDF correspondant
au chapitre : 110 Ko)
- H.M.T. et érosions ensemblistes
- Adjonction (I)
- Adjonction (II)
- Représentation et semi-groupes
- Cas d'un éspace E muni d'un translation
- dilatation d'ensembles et addition de Minkowski
- Erosion d'ensembles et soustraction de Minkowski
- Les deux dualités
- Propriétés algébriques des opérateurs de
Minkowski
- Addition de Minkowski par des convexes
- Effets de bords
- Dilatation et érosion standards
- Noyau des t-applications
- Equivalences entre ensembles et fonctions
- Dilatation d'une fonction par un élément
structurant plan
- Propriétés de operations planaires
- Eléments structurants non planaires
- Dilatation de fonctions par des éléments non
plans
- Résidus de transformations
- Résidus pour les ensembles et les fonctions
- Gradients morphologiques digitaux
- Gradient laplacien morphologiques (digitaux)
|
III - Ouvertures, fermetures
(cliquer pour télécharger le document PDF correspondant
au chapitre : 156 Ko)
- Ouverture et fermeture par adjonction
- Propriétés de l'ouverture par adjonction
- Effets de l'ouverture sur les ensembles
- Effets de la fermeture sur les ensembles
- Effets sur les fonctions
- Ouvertures et fermeture algébriques
- Invariants
- Représentations des ouvertures
- Suprema d'ouvertures
- Top hat (chapeau haut de forme)
- Propriétés du top hat
- Utilisation du top hat
- Exemple de top hat
- Granulométrie : point de vue intuitif
- Granulometrie : point de vue théorique
- Exemple de granulométrie
- Granulométrie et mesures
- Spectre granulométrique
|
IV - Filtrage morphologique
(cliquer pour télécharger le document PDF correspondant
au chapitre : 253 Ko)
- Définition des filtres morphologiques (I)
- Définition des filtres morphologiques (II)
- Construction des filtres morphologiques
- Filtres alternés (I)
- Filtres alternés (II)
- Relation d'ordre entre le compositions
- Comparaison entre
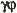 et et 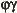
- Extension du top hat
- Inf-filtre, sup-filtre et filtre fort
- Interprétations géométriques
- Filtres alternés Séquentiels (I)
- Filtres alternés Séquentiels (II)
- Propriétés des filtres alternés séquentiels
- Usage des filtres alternés séquentiels (I)
- Usage des filtres alternés séquentiels (II)
- Usage des filtres alternés séquentiels (III)
- Pyramides
- Exemple de pyramide
- Le semi groupe
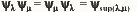
- Combinaison par sup et inf
- Centre morphologique
- Propriétés du centre morphologique
- Opérateur de contraste
- Le treilles de l'activité (ensembles)
- Le treilles de l'activité (fonctions)
|
V - Connexions ensemblistes
(cliquer pour télécharger le document PDF correspondant
au chapitre : 336 Ko)
- Connexité topologique (rappel)
- Critique
- Connexion
- Ouverture connexe ponctuelle
- Commentaires
- Exemples de connexions
- Connexion seconde par dilatation
- Application : recherche d'objets isolés
- Les maisons à grand jardin
- Connexions dans une séquence
- Connexion seconde par fermeture
- Connexion seconde par ouverture
- Connexion par partition
- Propriétés des connexions
- Préservation de la connexion
- Les transformations géodésiques
- Distance géodésique
- Boules géodésiques
- Dilatation géodésiques
- Erosion géodésique
- Dilatation géodésique digitale (binaire)
- Ouverture par reconstruction
- Connexion et ouverture par reconstruction
- Fermeture par reconstruction, treillis
- filtrage par érosion-reconstruction
- Elimination des grains touchant les bords
- Bouchage de trous
- Analyse individuelle de particules
- Application : extraction d'objet 3D (I)
- Application : extraction d'objet 3D (II)
- Connexité et reconstruction
- Géodésie et connexions
- Nice : alignements directionnels
|
VI - Connexions et fonctions numériques
(cliquer pour télécharger le document PDF correspondant
au chapitre : 899 Ko)
- Passage au numérique
- Treillis de fonctions (rappel)
- Treillis des partitions (rappel)
- Connexions induites par des fonctions
- Connexion lisse
- Exemple de connexion lisse
- Connexion par sauts
- Exemple de connexion par sauts
- Opérateurs connexes
- Opérateurs connexes, planaires, et croissants
- Dilatations géodésiques numériques (I)
- Dilatations géodésiques numériques (II)
- Reconstruction numérique
- Erosion reconstruction
- Application à l'examen du fond de l'oeil
- Swamping (reconstruction par marqueurs)
- Exemple de swamping : ouverture de contraste
- Maxima et ouverture de contraste
- Filtres forts par reconstruction
- Semi-groupes de filtres par reconstruction
- Exemple d'une pyramide de F.A.S. connexes
- Adjacence
- Nivellements
- Propriétés des nivellements
- Exemple de nivellement
- Dualité pour les fonctions
- Exemple de dualité
- Nivellement comme fonctions du marqueur
- Exemple de pyramide
- Exemple de réduction de bruit
|
VII - Squelettes (cliquer
pour télécharger le document PDF correspondant au
chapitre : 80 Ko)
- Résidus de familles de primitives
- Choix des familles de primitives
- Exemple de familles : famille homogène
- Exemple de familles : famille hétérogène
- Erosion ultime digitale (I)
- Erosion ultime digitale (II)
- Etrémités d'une particule
- Boules maximales
- Squelette : définition
- Squelette : construction
- Squelette : algorithme
- Squelette : propriétés (I)
- Reversibilité du squelette
- Squelette : propriétés (II)
- Bissectrice conditionnelle
- Bissectrice conditionnelle : construction
- Bissectrice conditionnelle : algorithme
- Récapitulatif des résidus de deux familles des
primitives
|
VIII - Amincissements
(cliquer pour télécharger le document PDF correspondant
au chapitre : 79 Ko)
- transformation par tout ou rien
- Amincissement - Epaississement
- Propriétés
- Homotopie pour les ensembles
- Homotopies pour les fonctions numériques
- Transformation homotopiques
- Homotopie et connexité dans le cas digital
- Connéxité en maille carrée (I)
- Connéxité en maille carrée (II)
- Connéxité en maille hexagonale
- Amincissements et épaississiments homotopiques
- Amincissements et épaississiments séquentiels
- Exemple d'amincissement séquentiel
- Propriétés des amincissements séquentiels
- Liste des éléments strucurants principaux, en
hexagonal
|
IX - Skiz et ligne de partage des
eaux (cliquer pour télécharger le document
PDF correspondant au chapitre : 121 Ko)
- Le squelette par zones d'influence : skiz
- Skiz géodésique
- Propriétés du skiz
- Les deux problèmes de la segmentation (I)
- Les deux problèmes de la segmentation (II)
- Fonction distance : définition
- Fonction distance : propriétés
- Exemple de fonctions distance
- Autre exemple
- Segmentation fine et fonction distance
- L.P.E d'un fonction numérique
- Construction de la L.P.E. par inondation (I)
- Construction de la L.P.E. par inondation (II)
- Construction de la L.P.E. par inondation (III)
- Exemple de la L.P.E. par inondation (I)
- Exemple de la L.P.E. par inondation (II)
|
X - Segmentation (cliquer
pour télécharger le document PDF correspondant au
chapitre : 508 Ko)
- Trois exmples
- Paradigme de segmentation morphologique
- Variables d'entrée
- Sélection des minima : filtrage
- Changement des minima : swanping
- Exemple critique des électrophorèses
- Electrophorèses : minima
- Electrophorèses : zones d'influence
- Electrophorèses : L.P.E. du gradient (I)
- Electrophorèses : L.P.E. du gradient (II)
- Electrophorèses : contours
- Electrophorèses : effets de bords
- Enseignements tirés de l'exemple
- Segmentation d'une chausée (I)
- Segmentation d'une chausée (II) : images synthétiques
- Segmentation d'une chausée (III) : marqueurs
- Segmentation d'une chausée (IV) :
conditionnalisation
- Segmentation d'une chausée (V) : résultats
- Enseignements tirés de l'exemple
- Image mosaïque : principe
- Image mosaïque : exemple
- L.P.E. d'une image mosaïque
- Pyramide de L.P.E. et d'image mosaïque (I)
- Pyramide de L.P.E. et d'image mosaïque (II)
- Pyramide de L.P.E. et d'image mosaïque (III)
|
XXI - Mesures (cliquer
pour télécharger le document PDF correspondant au
chapitre : 289 Ko)
- Fonctionnelles ensemblistes
- Modèle et notations
- Caractéristique d'Euler-Poincaré dans R1
- Caractéristique d'Euler-Poincaré dans R2
- Caractéristique d'Euler-Poincaré dans R3
- Propriétés de la C.E.P.
- Fonctionnelles de Minkowski
- Fonctionnelles de Minkowski dans R1 et R2
- Stéréologie
- Fonctionnelles de Minkowski dans R3
- Formules de Steiner pour les convexes
- Formules de Steiner, cas particuliers
- Individus et pondérations : volumes
- Individus et pondérations : nombres
- Généralisation aux fonctions numériques
- Quid de l'homogénéité ?
- Diomensionalité
- Périmètre et gradientNombre de connexité et dénivelés
- Autres mesures
- Nombre de convexité
- Dimensions fractales (I)
- Dimensions fractales (II)
- Dimensions fractales : exemple
|
XXII - La covariance (cliquer
pour télécharger le document PDF correspondant au
chapitre : 329 Ko)
- Covariance géométrique
- Erosion par un bipoint : exemple
- Anisotropies du covariogramme
- Versions probabilistes
- Cadre probabilistes stationnaire
- Covariance ensembliste
- Propriétés de la covariance ensembliste
- Pseudo-periodicités et covariance
- Groupements et covariance
- Bruit et covariance
- Covariance rectangle
- Propriétés de la covariance rectangle
- Exemple métallographique
- Passage des ensembles aux fonctions
- Comportements près de l'origine (I)
- Comportements près de l'origine (II)
- Comportements près de l'origine (III)
- Fonctions aléatoires de dilution
- Covariance et analyse spectrale
- Variance et portée
- Théorie intrinsèque, variogramme
- Exemple : marches poissonniennes (I)
- Exemple : marches poissonniennes (II)
- Clap de fin (I)
- Clap de fin (II)
|
XXIII - Erosion linéaire
(cliquer pour télécharger le document PDF correspondant
au chapitre 716 Ko)
- Erosion linéaire et covariance
- Le moment P(h)
- Erosion linéaire : exemple
- Quelques propriétés (I)
- Quelques propriétés (II)
- Individus et pondérations
- Poids, echantillonage, et stéréologie
- Granulometries linéaires en nombre et en mesure
- Exemple de distribution f(h) et g(h)
- Passage au cas stationnaireL'étoile
- Interprétation géométrique
- Granulométrie de sphères
- Comportement à l'origine : courbure
- Comparaison de quattre écritures
- Comportement à l'origine : rugosité
- Exemple de rugosité
|
XXIV - Ensembles booléens
(cliquer pour télécharger le document PDF correspondant
au chapitre : 780 Ko)
- Notations et rappels
- Construction de fermés bolléens
- Exemples de fermés booléens (I)
- Exemples de fermés booléens (II)
- Fonctionnelle caractéristique Q(B); (I)
- Fonctionnelle caractéristique Q(B); (II)
- Quelques Q(B) particuliers
- Propriétés ensemblistes
- Exemple de stabilité pour la réunion
- Exemple de stabilité pour la dilation
- E.F.A. indéfiniment divisible (I)
- E.F.A. indéfiniment divisible (II)
- Théorème de limite centrale
- Grains primaires convexes (I)
- Grains primaires convexes (II)
- Exemple de cokes moulés (I)
- Exemple de cokes moulés (II)
- E.F.A. semi-markoviens (I)
- E.F.A. semi-markoviens (II)
- Granulométries linéaires
- Comment tester un E.F.A. booléen ?
- Test d'une simulation booléene (I)
- Test d'une simulation booléene (II)
- Test d'une simulation booléene (III)
- Relations stéréologiques
- Antinomie "nucléation-croissance" (I)
- Antinomie "nucléation-croissance" (II)
- Modèle dérivé : structures triphasiques
- Exemple : agglomérés de minerai de fer
- Usage heuristique du modèle booléen (I)
- Usage heuristique du modèle booléen (II)
|
XXV - Tesselation aléatoires
(cliquer pour télécharger le document PDF correspondant
au chapitre : 688 Ko)
- Moments en nombre et en mesure
- Poids, échantillonage et stéréologie
- Tesselations aléatoires
- Droites poissoniennes
- Propriétés élémentaires
- Moments
- Fonctionnelles caractéristique Q(K); (I)
- Fonctionnelles caractéristique Q(K); (II)
- Les polyèdres de Poisson sont amnésiques
- Exemples de droites de Poisson
- E.F.A. stables pour la réunion dans Rn
- Trajectoire browniennes et capacité newtonienne
- Doublets poissonniens (I)
- Doublets poissonniens (II)
- E.F.A. booléens - poissoniens
- Exemples d'E.F.A. booléens - poissoniens
- Voronoï et Johnson-Mehl (I)
- Voronoï et Johnson-Mehl (II)
- Exemple de Johnson-Mehl
- Tesselation quasi-périodiques
- Exemples de tesselation quasi-périodiques
|
XXVI - Fonctions booléennes
(cliquer pour télécharger le document PDF correspondant
au chapitre : 385 Ko)
- Fonctions aléatoires considérées comme E.F.A.
- Treillis des fonctions s.c.s.
- Propriétés topologiques des fonctions s.c.s.
- Fonctions aléatoires s.c.s. (G. Matheron, 1969)
- Notations pour le cas bi-dimensionnel
- Construction des îlots booléens
- Exemples de'îlots booléens
- Fonctionnels caractéristique Q(K)
- Moments (I)
- Moments (II)
- Îlots booléens et convexité
- Fonctions booléennes asymptotiques : les fonds
rocheux
- Exmples de fonds rocheux
- Fonctionnelle Q(K) des fonds rocheux
- Prototypes de fonctions booléennes
- Propriétés ensemblistes
- Îlots booléens et stéréologie
- Usage des fonctions booléennes
- Exemple : simulations de facies entrecoisés
- Exemple de comptage
- Applications des fonctions booléennes
|
|